Page 12 - NCERT Books

100 MATHEMATICS

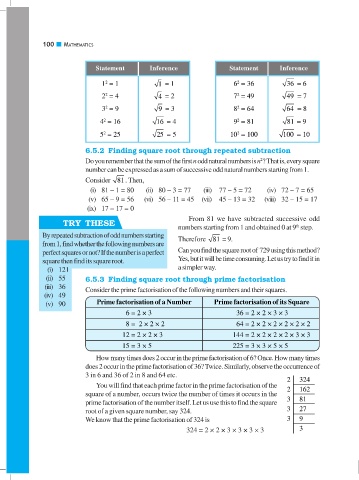
Statement Inference Statement Inference

2
2
1 = 1 1 = 1 6 = 36 36 = 6
2
2
2 = 4 4 = 2 7 = 49 49 = 7
3 = 9 9 = 3 8 = 64 64 = 8
2
2
2
2
4 = 16 16 = 4 9 = 81 81 = 9
5 = 25 25 = 5 10 = 100 100 = 10
2
2
6.5.2 Finding square root through repeated subtraction
2
Do you remember that the sum of the first n odd natural numbers is n ? That is, every square
number can be expressed as a sum of successive odd natural numbers starting from 1.
Consider 81. Then,
(i) 81 – 1 = 80 (ii) 80 – 3 = 77 (iii) 77 – 5 = 72 (iv) 72 – 7 = 65
(v) 65 – 9 = 56 (vi) 56 – 11 = 45 (vii) 45 – 13 = 32 (viii) 32 – 15 = 17
(ix) 17 – 17 = 0
From 81 we have subtracted successive odd
TRY THESE
numbers starting from 1 and obtained 0 at 9 step.
th
By repeated subtraction of odd numbers starting
Therefore 81 = 9.
from 1, find whether the following numbers are
perfect squares or not? If the number is a perfect Can you find the square root of 729 using this method?
square then find its square root. Yes, but it will be time consuming. Let us try to find it in
(i) 121 a simpler way.
(ii) 55 6.5.3 Finding square root through prime factorisation
(iii) 36
Consider the prime factorisation of the following numbers and their squares.
(iv) 49
(v) 90 Prime factorisation of a Number Prime factorisation of its Square
6 = 2 × 3 36 = 2 × 2 × 3 × 3

8 = 2 × 2 × 2 64 = 2 × 2 × 2 × 2 × 2 × 2
12 = 2 × 2 × 3 144 = 2 × 2 × 2 × 2 × 3 × 3
15 = 3 × 5 225 = 3 × 3 × 5 × 5

How many times does 2 occur in the prime factorisation of 6? Once. How many times
does 2 occur in the prime factorisation of 36? Twice. Similarly, observe the occurrence of
3 in 6 and 36 of 2 in 8 and 64 etc.
2 324
You will find that each prime factor in the prime factorisation of the
2 162
square of a number, occurs twice the number of times it occurs in the
3 81
prime factorisation of the number itself. Let us use this to find the square
root of a given square number, say 324. 3 27
We know that the prime factorisation of 324 is 3 9
324 = 2 × 2 × 3 × 3 × 3 × 3 3