Page 5 - LN

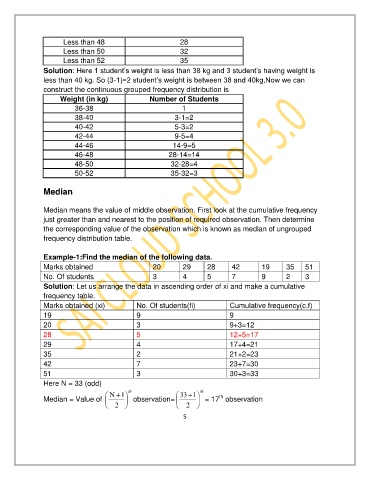
Less than 48 28
Less than 50 32
Less than 52 35
Solution: Here 1 student’s weight is less than 38 kg and 3 student’s having weight is
less than 40 kg. So (3-1)=2 student’s weight is between 38 and 40kg,Now we can
construct the continuous grouped frequency distribution is
Weight (in kg) Number of Students
36-38 1
38-40 3-1=2
40-42 5-3=2
42-44 9-5=4
44-46 14-9=5
46-48 28-14=14
48-50 32-28=4
50-52 35-32=3

Median

Median means the value of middle observation. First look at the cumulative frequency
just greater than and nearest to the position of required observation. Then determine
the corresponding value of the observation which is known as median of ungrouped
frequency distribution table.

Example-1:Find the median of the following data.
Marks obtained 20 29 28 42 19 35 51
No. Of students 3 4 5 7 9 2 3
Solution: Let us arrange the data in ascending order of xi and make a cumulative
frequency table.
Marks obtained (xi) No. Of students(fi) Cumulative frequency(c.f)
19 9 9
20 3 9+3=12
28 5 12+5=17
29 4 17+4=21
35 2 21+2=23
42 7 23+7=30
51 3 30+3=33
Here N = 33 (odd)
 N 1  th  33 1  th
th
Median = Value of   observation=   = 17 observation
 2   2 
5