Page 3 - Lesson note-7 Extra Questions Ch.10 Circle

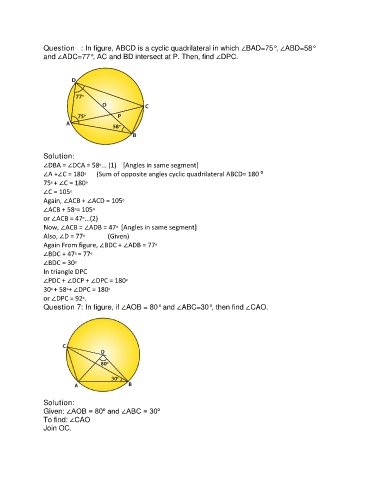
Question 6: In figure, ABCD is a cyclic quadrilateral in which ∠BAD=75°, ∠ABD=58°
and ∠ADC=77°, AC and BD intersect at P. Then, find ∠DPC.

Solution:
∠DBA = ∠DCA = 58⁰... (1) [Angles in same segment]

∠A +∠C = 180⁰ (Sum of opposite angles cyclic quadrilateral ABCD= 180 ⁰
75⁰ + ∠C = 180⁰
∠C = 105⁰
Again, ∠ACB + ∠ACD = 105⁰
∠ACB + 58⁰= 105⁰
or ∠ACB = 47⁰...(2)

Now, ∠ACB = ∠ADB = 47⁰ [Angles in same segment]
Also, ∠D = 77⁰ (Given)
Again From figure, ∠BDC + ∠ADB = 77⁰
∠BDC + 47⁰ = 77⁰
∠BDC = 30⁰
In triangle DPC

∠PDC + ∠DCP + ∠DPC = 180⁰
30⁰ + 58⁰+ ∠DPC = 180⁰
or ∠DPC = 92⁰.
Question 7: In figure, if ∠AOB = 80° and ∠ABC=30°, then find ∠CAO.

Solution:
Given: ∠AOB = 80⁰ and ∠ABC = 30⁰
To find: ∠CAO
Join OC.