Page 2 - LN

The graph of a quadratic polynomial is a parabola. The roots of a quadratic equation are
the points where the parabola cuts the x-axis i.e. the points where the value of the
quadratic polynomial becomes zero.

Graphically, the roots of a quadratic equation are the points where the graph of the
quadratic polynomial cuts the x-axis.

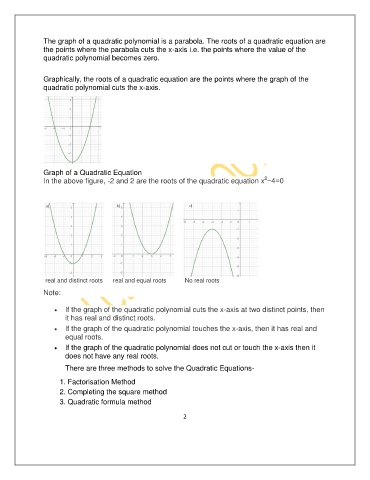
Graph of a Quadratic Equation
2
In the above figure, -2 and 2 are the roots of the quadratic equation x −4=0

real and distinct roots real and equal roots No real roots

Note:

 If the graph of the quadratic polynomial cuts the x-axis at two distinct points, then
it has real and distinct roots.
 If the graph of the quadratic polynomial touches the x-axis, then it has real and
equal roots.
 If the graph of the quadratic polynomial does not cut or touch the x-axis then it
does not have any real roots.

There are three methods to solve the Quadratic Equations-

1. Factorisation Method
2. Completing the square method
3. Quadratic formula method

2