Page 2 - Worksheet 1 Ch.10 Circle
P. 2
Answer the following
6 How many circles can be drawn through 3 non collinear points? 1
7 What do mean by circum center? 1
Section B
8 If the perpendicular bisector of a chord AB of a circle PXAQBY intersects the circle at P 2
and Q, prove that arc PXA = arc PYB.
9 AB and AC are two equal chords of a circle. Prove that the bisector of the angle BAC 2
passes through the centre of the circle.
10 If a line segment joining mid-points of two chords of a circle passes through the centre 2
of the circle, prove that the two chords are parallel.
Section C
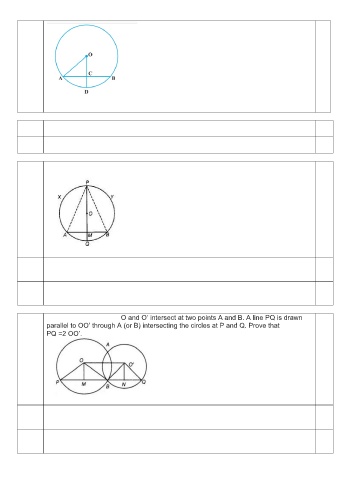
11 Two circles with centers O and O’ intersect at two points A and B. A line PQ is drawn 3
parallel to OO’ through A (or B) intersecting the circles at P and Q. Prove that
PQ =2 OO’.
12 If two equal chords of a circle intersect, prove that the parts of one chord are separately 3
equal to the parts of the other chord
13 If two chords AB and CD of a circle AYDZBWCX intersect at right angles, then prove 3
that arc CXA + arc DZB = arc AYD + arc BWC = semi-circle.